The value and importance of the clinician's ability to identify the presence of a disease in a patient and to prescribe effective medical treatment on that basis needs no explanation. And, of course, such abilities are diagnostic and prognostic in character. But what is diagnosis? It seems clear enough that diagnosis is a matter of judgement. However, it is also perfectly clear that to say this is really to say very little. What kind of judgement is diagnostic judgement? And how are such judgements arrived at? Making a diagnostic judgement can be a relatively simple matter, e.g. self-diagnosis of a common cold. But the domain of diagnostic judgement extends across the whole of the disease taxonomy, from the common cold through states of organs, anatomical structures and the immune system, to pathogenic factors, i.e. to the foundations of biology. Properly understood, then, diagnostic judgement is scientific judgement and, indeed, expert diagnostic judgement is scientific judgement par excellence.

Given the scientific character of diagnostic judgement, it is surprising that the nature of the diagnostic process has been so little scrutinised by contemporary philosophers of science. ¹ Moreover, given the unique importance of diagnosis to the practice of medicine, it is even more surprising that the study of diagnosis should continue to make so small a contribution to standard medical curricula. Traditional attitudes to diagnosis as a 'process of intuition' or arcane 'natural art' ² go a long way towards explaining this situation. Certainly, such attitudes do nothing to clarify the nature of diagnostic skills (or to promote their teachability). The practical importance of a clear and communicable understanding of the nature of such skills is most pungently illustrated in any case of misdiagnosis, the net result of which may be tragic.

Further, my point about the role and status of diagnosis in the practice of medicine is not simply that diagnosis (along with prognosis and treatment) is one of the triumvirate of processes which are traditionally construed as definitive of general practice but rather that, as the Royal College of General Practitioners noted in 1972, a correct diagnosis: "..is a crucial achievement which opens the way to prognosis and treatment." ³ Hence, the diagnostic process generally enjoys a significant logical priority in medical practice. ⁴ For all these reasons, it is particularly important to have a clear picture of the way in which diagnoses are (or, at least, ought to be) arrived at. How should scientific judgements of this kind be made? My primary purpose in this paper is to try to give an answer to exactly that question. Further, if I fail to nail down exactly what the logic of diagnosis is, I hope at least to conclusively establish what the logic of diagnosis cannot be.

A popular and concise definition, due to Feinstein, describes diagnosis as "a process of converting evidence into the names of diseases". ⁵ But what exactly is the nature of that process? If diagnosis is a rational process then possible answers to this question are constrained by epistemology itself, i.e. by the traditional (allegedly exhaustive) epistemological classification of rational inferences as either inductive or deductive. In what follows, I will assume that diagnosis is a rational process. Hence, there are three possibilities:

(i) Diagnostic reasoning is exclusively inductive.

(ii) Diagnostic reasoning is exclusively deductive.

(iii) Diagnostic reasoning involves both induction and deduction.

A little reflection will quickly reveal that neither (i) nor (ii) represent defensible positions. It follows that the correct account of diagnostic reasoning is given by (iii).

I establish that conclusion here as follows: first, by showing that any specifically Popperian Falsificationist account is inadequate and second, by showing that, although diagnosis undoubtedly involves deduction, any purely deductivist account of diagnostic reasoning must be incomplete precisely because it excludes inductive reasoning. In order to usefully consider any such account, however, we require something of a picture of the diagnostic process first.

The process of diagnosis is often a complex one involving a large number of variables and, frequently, variables of different kinds. Relevant factors can be physical but, equally, they may be social and/or psychological in character. At least one account of diagnostic method, Marshall Marinker's (1981) account, the method of 'Triple Diagnosis', requires that physical, social and psychological factors all be taken into account (as appropriate) in every case of diagnosis. ⁶ Nonetheless, diagnosis develops through clearly identifiable stages which allows us to sketch the diagnostic process (with very broad brush strokes) as follows:

(i) Diagnosis begins with symptoms, i.e. diagnosis begins when symptoms are presented by a patient in a medical context, e.g. in a general practice or at a hospital clinic. Frequently, the kind of context in which symptoms are presented is itself a significant factor in the diagnostic process. As Fraser (1987) notes, for example, the diagnostic outcomes for presentation of a cough in the context of a general practice differ markedly from the diagnostic outcomes for presentation of a cough in the context of a hospital chest clinic. ⁷

(ii) In the light of the symptoms presented, the clinician will generate a finite list of relevant diagnostic hypotheses. Usually, this will be a very short list indeed. As Macartney (1995) notes: "There seems to be good evidence that the limited short term memory of the clinician means that the number of hypotheses entertained at any one time is restricted to four +/- one." ⁸

(iii) The clinician attempts to use all available evidence to discriminate between the relevant hypotheses, i.e. both to effectively eliminate any incorrect hypotheses and to endorse possibly correct hypotheses.

(iv) In the ideal case, the process of discrimination will result in isolating a single diagnostic hypothesis as the correct one.

(v) Consequently, an explanation of presenting symptoms can be given in the light of the relevant diagnosis, a prognosis can be made and an appropriate course of treatment identified.

With this very brief sketch in mind we can go on to ask just which kind or kinds of reasoning are involved at each stage? To get an answer to that question it is natural to consult standard medical texts in the area. So, for example, we might usefully consider the account of the diagnostic process given by Robin C Fraser (1987) in his Clinical Method: A General Practice Approach. ⁹ Fraser writes to intending GP's as follows: "It is likely that you will have been taught to reach a diagnosis by using the traditional or inductive method of problem solving." ¹⁰ That this is not Fraser's own view is made clear in the following remarks:

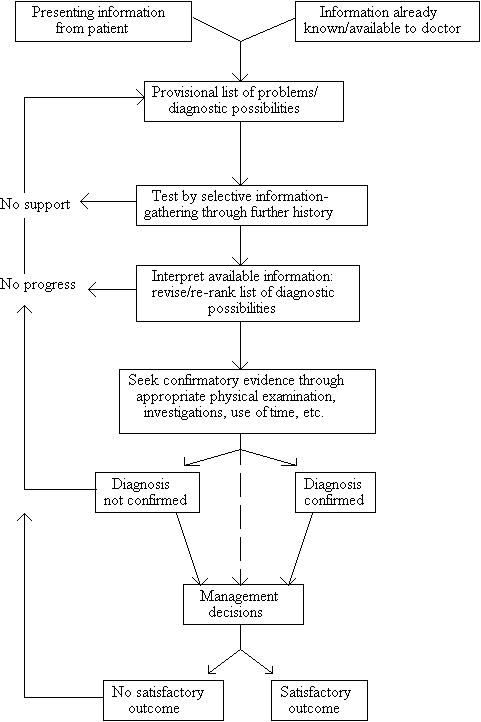
In actual clinical practice, however, such an approach to clinical problem-solving is rarely used by general practitioners and infrequently used by hospital doctors because it lacks discrimination and has a poor yield in terms of the time and effort expended....In reality, most clinicians reach diagnosis by a process of hypothetico-deductive reasoning, i.e. by educated guessing and testing. ¹¹

The most recent Oxford Dictionary of Philosophy (1994) describes the hypothetico-deductive method as: "The method particularly associated with a philosophy of science that stresses the virtues of falsification." ¹³ The definitive account of scientific method which 'stresses the virtues of falsification' is Popperian Falsificationism and, therefore, it is tempting to consider Fraser's (1987) account of method to be a Popperian one. But that would surely be a mistake. Fraser's (1987) account of method cannot possibly be the Popperian one. The point can be seen clearly in terms of the flow-chart by focusing on the fifth and sixth steps where Fraser (1987) urges the clinician to seek confirmatory evidence in order to confirm or disconfirm diagnostic hypotheses. The notion of confirmation, however, is inherently inductivist: it is the idea that there can be degrees of inductive support for hypotheses, proportionate to the number and type of test which the hypothesis has survived. Just as more and more observation-statements as premises in an inductive argument seem to offer increasing degrees of support for their conclusion so more and more confirmations seem to increase the likelihood of a hypothesis being true, i.e. better confirmed hypotheses are more likely to be true.

Hence, to recognise support in terms of degrees of confirmation is to embrace inductivism. As such, the notion of confirmation is anathema to Popper. As Popper (1963) most famously puts the point: "Induction, i.e. inference based on many observations, is a myth." ¹⁴ Further, the notion of confirmation is typically explicated by appeal to the notion of probability. But, again, throughout his career, Popper consistently and completely rejected probabilistic accounts of scientific method. Indeed, (together with David Miller) Popper (1983) maintained that probabilistic induction is impossible precisely because confirmation itself is impossible. ¹⁵ Hence, as regards reporting and assessing the results of test-survival by hypotheses, Popper (1959) replaced the inductivist notion of degree of confirmation with a non-inductivist notion of degree of corroboration. Notably, that notion is described by Popper (1959) as one of the two most important 'logical tools' developed in The Logic of Scientific Discovery. ¹⁶ Corroboration, however, is only a measure of the number and type of tests survived by a hypothesis, i.e. in sharp contrast to the forward-looking idea of confirmation, corroboration is always and only backward-looking and has no predictive content. As Popper himself puts the point:

It follows that Fraser's (1987) version of the hypothetico-deductive method is not identical with Popper's. And, surely, that is just as well. For, given Popper's account of test-survival, it is quite clear that Popper cannot possibly give an adequate account of diagnostic reasoning. This is easily shown.

Suppose that I go to my local GP (who is a great admirer of Poppers' work and a dedicated Falsificationist) about my cough, i.e. I go along to my local general practice presenting my cough as symptom. Further suppose that, in his wisdom, my GP decides to entertain a list of the following ten diagnostic hypotheses: Acute bronchitis, Common cold, Influenza, Chronic bronchitis, Laryngitis, Pneumonia, Whooping cough, Measles, Pulmonary tuberculosis and, finally, lung cancer. For simplicity, we may refer to these diagnostic hypotheses as {d₁......d₁₀}. Now suppose that, after a certain amount of time, a given amount of relevant information has been amassed and a number of appropriate tests have been conducted. As a result, let's say, half the hypotheses, {d₆......d₁₀}, for example, have been falsified and the remaining hypotheses {d₁......d₅} have been assigned appropriate degrees of corroboration. As noted, a correct diagnosis will make possible both prognosis and treatment, i.e. the practical value of a correct diagnosis consists precisely in establishing a basis for correctly predicting the future course of the disease. So, which hypothesis from {d₁......d₅} should the Popperian GP select for that predictive purpose?

In other words, has Popper provided any rational, non-inductivist, basis for preferring one such hypothesis to another for prognostic purposes? Accurate prediction is crucially important here and if Popper can give no rationale for hypothesis-selection for prognostic purposes then he cannot give a complete account of diagnostic reasoning.

There may well seem to be a very obvious, very Popperian, answer here, i.e. that Popper's reply to the question: on what basis should we choose among surviving hypotheses for purposes of prediction should be to give the following simple advice: choose the best corroborated hypothesis. But this will not do. Corroboration is not confirmation. And to assess hypotheses for predictive purposes on the basis of degrees of corroboration is, by Popper's own admission, to assess predictiveness by a criterion which emphatically lacks any predictive content. Earlier, I noted Popper's attitude to corroboration in his seminal early work The Logic of Scientific Discovery but it is important to appreciate that Popper's commitment to that conception is continuous throughout his writing. Hence, in his much later Autobiography we find the same commitment to the same concept. Again, in Popper's own words:

Throughout his discussion of the hypothetico-deductive method Fraser (1987) speaks of 'confirming diagnostic probabilities' and, therefore, Fraser's (1987) understanding of the method differs markedly from Popper's. Further, of that method, the Oxford Dictionary of Philosophy (1994) also describes a: "philosophical divide .. between radical followers of Popper who deny that probability accrues to a theory through its having survived such tests, and others who insist that it must." ²¹

In these terms, then, Fraser (1987) is one of the 'others'. But how useful is it to describe any such account of method as hypothetico-deductive? If, as it does, Fraser's (1987) account of method allows the assignment of probability-values to hypotheses and allows degrees of probability to accrue to hypotheses in ways which satisfy the axioms and theorems of the probability-calculus then Fraser's (1987) is an inductivist account of method.

Certainly, it must be a mistake to apply the term 'hypothetico-deductive' equally to both Popper's account and to Fraser's (1987). For, on this view of the method, every account of scientific method which accepts as valid inferences by modus tollens, i.e. every rational account of scientific method, is hypothetico-deductive. Therefore, simply classifying an account of method as hypothetico-deductive so far gives us no basis to distinguish between purely deductivist accounts such as Popperian Falsificationism and standard inductivist accounts such as Bayesianism. The fact that two such radically different accounts of the logic of scientific method might be represented as but two versions of a single kind of method is at best misleading and at worst false.

It is possible that what is meant by calling both accounts hypothetico-deductive is that both agree in prohibiting inductive reasoning to relevant hypotheses in the first place, i.e. in prohibiting the inductive generation of hypotheses. In the present context, however, this claim is quite false. Fraser (1987) explicitly encourages the inductive generation of hypotheses. And, indeed, if he did not, it would be wholly unclear why inductive reasoning should be permitted as regards the confirmation of hypotheses but prohibited as regards the generation of hypotheses, i.e. inductive reasoning either is legitimate (in which case there seems to be no reason why we should not generate hypotheses inductively in the first place) or it is not (in which case we would have to give up on a theory of confirmation).

In sharp contrast, the Popperian will be forced to attempt such a prohibition. Hence, the Popperian account can again be seen to be an inadequate account of diagnostic reasoning. For, as the study of valid inference, deductive logic merely concerns relations between sentences. Therefore, deduction alone cannot establish the content of any factual truth. Certainly, deductive logic can tell us that a given sentence must be true if some other sentences are true but it cannot possibly be by deductive means that we establish the truth of those sentences in the first place. Thus, if inductive reasoning is prohibited as regards the generation of hypotheses then, given the epistemological dichotomy, it follows that every initial set of diagnostic hypotheses must be arrived at in a way which is entirely devoid of any rational inferential structure. In other words, it follows that the process of generation of hypotheses is not rationally analysable at all. But what might such a process be? If reason is wholly excluded at this stage, the process of generating hypotheses must be left to imagination. But the claim that GP's and hospital doctors invariably generate every set of diagnostic hypotheses by acts of sheer imagination is certainly false, perhaps even bizarre. Yet this would appear to be the only explanatory line open to any purely deductivist account of diagnostic reasoning such as the one proposed by the Popperian Falsificationist.

To appreciate that the claim in question is false we need only consider the set of diagnostic hypotheses outlined earlier for the presenting symptom of a cough in the context of a general practice. If the members of that set had an intuitive relevance and plausibility that is undoubtedly due to that fact that medical research ²² has shown that these ten hypotheses, in the order given, account, in sum, for 93% of diagnostic outcomes in that context, given that presenting symptom. Hence, the hypothetical GP could simply have generated the relevant set of initial diagnostic hypotheses on the basis of recorded frequencies of diagnostic outcomes among a relevant population of patients (I am not suggesting that this is the only way in which initial hypotheses might be generated, merely that this is one rational method). Moreover, the rationale for generating diagnostic hypotheses in this way consists precisely in the attempt to identify the most plausible potential explanations for the presenting symptom as quickly as possible. Therefore, we can fairly describe the GP's strategy in so doing as one of inference to the best (loveliest potential) explanation, given that presenting symptom. ²³

Unsurprisingly, in his discussion of the process of generating and ranking appropriate diagnostic hypotheses, Fraser (1987) identifies probability as the single most important factor in that process since: "in any given clinical circumstance the essential question a doctor must ask is: What is the most likely cause(s) of my patient's symptoms?" ²⁴ and goes on to note that:

At the very least, it is surely clear that assigning the task of generating initial diagnostic hypotheses to imagination alone is not only potentially enormously wasteful of time and resources but also downright dangerous and potentially tragic. Moreover, it is also clear that the claim that the appropriate process (or that the actual process) for generating initial diagnostic hypotheses is one which is devoid of any rational inferential structure is patently false.

In the preceding Sections, I have tried to cast doubt upon the plausibility of any purely deductivist account of either the predictive aspects of diagnostic reasoning or of the process of generating diagnostic hypotheses. However, given its rejection of any inductivist notion of confirmation, pure deductivism can again be seen to be inadequate as regards a further aspect of diagnostic reasoning, for the pure deductivist has no means of representing gradations in the confirmation or disconfirmation of diagnostic hypotheses. It follows that pure deductivism can give no account of relative evidential value in terms of its effects on the clinician's degree of belief, i.e. no rational account of how a clinician's degree of belief in a diagnostic hypothesis should be affected by fresh empirical evidence which does not maximally confirm or disconfirm that hypothesis.

Consider, for example, the following case outlined by Wulff et al. (1986) in Philosophy of Medicine: An Introduction. ²⁶ In it, a clinician considers an initial diagnostic hypothesis to the effect that a given patient has a hepatocellular carcinoma. In an attempt to confirm this hypothesis the clinician performs a relevant test, namely, determination of alpha-fetoprotein in the serum. Suppose that the test is positive and that the clinician is aware that 70% of patients with hepatocellular carcinoma show a positive result as against 2% of patients who do not. The truth of the clinician's hypothesis is certainly not entailed by the result of the test but neither is the falsity of that hypothesis thereby established. For a pure deductivist, then, it would seem to follow that the clinician's degree of belief in the truth of the hypothesis should be unaffected. But that is highly counter-intuitive.

Surely, the probability of the hypothesis has been substantially increased and, therefore, the clinician's hypothesis is significantly confirmed. It is natural then to suppose that the clinician's degree of belief in the hypothesis should increase proportionately. But the problem is that, without a notion of confirmation, the pure deductivist can provide no rational explanation of that fact. In contrast, the inductivist can very readily give just such an explanation. Again, Fraser's (1987) insight that the notion of probability is crucial in the diagnostic process is exactly right. Gradations of confirmation (and thus relative evidential value) can easily be represented if we have recourse to a concept of probability which satisfies the rules and axioms of the probability calculus, i.e. to an inductivist theory of confirmation. Given such a theory we can easily represent the reasoning involved in this case formally and clearly express the relative value of the evidence gathered from the test as regards the initial hypothesis.

Consider what the clinician knows prior to the test, for example, namely, that 70% of patients with hepatocellular carcinoma show a positive result as against 2% of patients who do not. Where the positive result of the test is represented by 's' (for 'sign' or 'symptom'), the diagnosis by 'd' and the stroke '/' is understood in the usual way, these initial probabilities can be represented as follows:

What the clinician needs to know, of course, is not the probability of the sign given the disease but rather the probability of the disease given the sign, i.e. P(d / s). And that is what Bayes's Theorem allows him to compute. Consider, for example, Bayes's Theorem in the following form:


                                           P(s / d) . P(d)
P(d / s) =                       -------------------------------

                                    P(s / d) . P(d) + P(s / ~d) . P(~d)
 

The only unknown quantity in the equation is just the prior probability of the patient having the disease anyway. As noted in the previous Section, however, the clinician could simply compute the frequency of the disease in the population and adopt that result as the relevant prior. Hence, if that frequency is, say, 25% then the clinician may adopt 0.25 as the prior probability of the presence of the disease and, therefore, calculate the prior probability of the absence of the disease as 0.75, i.e.

Thus the clinician can exploit Bayes's Theorem in order to calculate the posterior probability of the diagnosis, i.e. P(d / s) = 0.92. Further, that result could now be construed as itself a prior probability for the purpose of conducting further tests. In other words, applications of Bayes's Theorem can be iterated as required. Hence, quite generally, the clinician can exploit Bayes's Theorem in order to represent the relative evidential value (i.e. degree of confirmation) of any test just in terms of the way in which the probability value of the original hypothesis is affected by the result of the test. But that strategy is not open to any purely deductivist account of diagnostic reasoning and, therefore, the purely deductivist account can again be seen to be an inadequate account of the nature of diagnostic reasoning.

Now it could be argued that both Bayes's Theorem itself and the application illustrated above are, in one sense, quite acceptable to pure deductivists such as Popper. After all, considered purely mathematically, the probability calculus in general and Bayes's Theorem in particular are quite uncontroversial and thus perfectly acceptable to all and sundry.

However, just as such, the calculus and Bayes's Theorem are empirically useless, i.e. in order to exploit the calculus and actually apply Bayes's Theorem we must offer an interpretation of the notion of probability involved and, indeed, an interpretation which satisfies the axioms and theorems of the probability calculus. But, it might be argued, Bayesianism is not the only interpretative option here. Certainly, probability-values could be understood subjectively, as measures of the clinician's degree of belief in a hypothesis but, in sharp contrast, a case might be made be for an objective account of probability, e.g. probability-values might be considered as belonging (in some sense) to a hypothesis or to a given experimental set-up rather than to any clinician. Further, while the former subjectivist option is anathema to Popper the latter (suitably specified) objectivist account might well be perfectly acceptable. Indeed, much of The Logic of Scientific Discovery is devoted precisely to the task of specifying an acceptable objectivist account (the Propensity Theory). Moreover, if we were to accept a frequency interpretation of probability Popperians might even get their methodological hands on the kind of reasoning outlined in Section IV above, i.e. as regards generating diagnostic hypotheses.

There are a number of points which need to be made here however. First, as is ably demonstrated (for example) by Howson and Urbach (1989), Popper's particular version of the Propensity Theory can readily be refuted reductio ad absurdum. ²⁷

Moreover, while much of the attraction of Popper's theory consisted in his claim that the theory affords important insights into quantum mechanical phenomena both Gibbins (1987) and Milne (1986) have shown that Popper's theory is in fact wholly inadequate in that regard. More generally, it seems fair to say that no objective interpretation of probability has ever been successful, not least because on any such analysis probability-values themselves turn out, ultimately, to be a priori, i.e. fail to be independent of the particular theory and/or language in which they are calculated. Admittedly, I have not proved these results here and it remains possible that an entirely successful objectivist account will emerge. As yet, however, this is nothing more than a possibility.

Further, as regards the illustration of hypothesis-generation in Section IV, I am not convinced that we do need to understand probability-values as objective even in that instance. First, recall that the point illustrated there was that initial diagnostic hypotheses could be generated in this way and, indeed, that this represented a rational, inferentially-structured procedure in contrast to the Popperian claim that the relevant process was not rationally analysable. Moreover, at that stage, while we are committed to the existence of frequencies in a population we are not yet committed to the existence of probabilities, prior or otherwise. In other words, the clinician arrives at a set of priors when the decision is taken to accept or adopt that set of diagnostic hypotheses as the relevant set of diagnostic probabilities. Nothing forces the clinician's hand here. Other hypotheses which, for example, represent much lower frequencies of diagnostic outcome, might well be included at the earliest stage. The effects of applying Bayes's Theorem in particular and satisfying the axioms of the probability-calculus generally ensures consistency and thus rationality. Hence, the process of diagnostic judgement can indeed be probabilistic precisely in the personalist sense all the way down. ²⁸

Finally, and most importantly, if we are concerned to represent the process of diagnostic judgement as rationally analysable then our primary concern is to represent the way in which the clinician's degree of belief in a hypothesis ought to be affected by evidence. But without a personalist, subjectivist account of probability there can be no question of explaining that. In other words, the objectivist has thrown the baby out with the bathwater and consequently can give no adequate account of relative evidential value as regards degrees of belief.

To argue against the defensibility of any purely deductivist account of the nature of diagnostic reasoning is not, however, to argue against deductive logic itself (I am certainly not disputing the validity of modus tollens here). Equally, I do not suggest that there is no place for intuition or imagination in the diagnostic process. Nothing could be further from the truth. Any adequate account of the diagnostic process should undoubtedly incorporate deductive logic and allow for imagination and intuition. However, the diagnostic process can be a rich and complex one involving ineradicable inductive elements which no purely deductivist account can hope to model. In other words, any deductivist account must remain an incomplete account. It follows that diagnostic reasoning is neither exclusively inductive nor exclusively deductive, i.e. diagnostic reasoning exploits both induction and deduction.

However, I have argued that the logic of diagnostic reasoning is best represented in terms of the theory of probability, i.e. the account of the logic of diagnostic reasoning which I have proposed here is essentially probabilistic. Moreover, as demonstrated above, only a subjectivist interpretation of the notion of probability can possibly be adequate to representing the actual process of diagnostic reasoning and, therefore, the nature of diagnostic judgement.

Further, I am not proposing a naively subjectivist account here but rather that probability values should be understood as a matter of the degree of rational belief appropriate to diagnostic hypotheses, i.e. a subjectivist account with, in gamblers' parlance, a definition of fair odds such as is given (for example) by Howson and Urbach (1989). Given such an interpretation, Bayes's theorem can easily be exploited to calculate the specific numerical posterior probability of any diagnostic hypothesis, i.e. the probability of that hypothesis in the light of given evidence. Thus, quite generally, Subjective Bayesianism gives a precise answer to the question: how should the clinician's degree of belief be affected by fresh empirical evidence? For general diagnostic purposes, the form of the theorem considered in the previous Section (i.e. the one cited from Wulff et al. 1986) is too severely restricted and, therefore, it is desirable to have a form of the theorem which applies quite generally to any number of diagnostic hypotheses.

Thus, where d₁, d₂, …, d_n are mutually exclusive and jointly exhaustive diagnostic hypotheses, and s is a given sign or symptom, the probability of a particular diagnosis d_k given s can be calculated using the following form of Bayes's Theorem:
 

                                     P(s / d_k ) . P(d_k)

P(d_k / s) =                   -------------------

                                     i = n

                                     S P(s / d_i) . P(d_i)

                                     i = 1
 

Given this, the general diagnostic form of Bayes's theorem, posterior probabilities can be calculated and distinguished from prior probabilities just in terms of changes in the clinician's degree of belief in a given diagnostic hypothesis in the light of new signs and/or symptoms, i.e.

(i) d_k is confirmed by s if and only if P(d_k / s) > P(d_k ).

(ii) d_k is disconfirmed by s if and only if P(d_k / s) < P(d_k ).

(iii) If d_k entails s then P(s / d_k ) = 1.

(iv) If d_k entails s then P(d_k / ~s) = 0.

Confirmation, disconfirmation, entailment and falsification are thus represented and, therefore, a formal Bayesian framework rich enough to model diagnostic reasoning has been provided. ²⁹

At this point, it is worth pre-empting two of the most obvious objections to a Subjective Bayesian account of diagnostic reasoning. The first concerns the problem of establishing prior probabilities for diagnostic hypotheses. The point may be put as follows: the hypothesis in question must already possess a prior probability of a finite, non-zero nature if evidence is ever to increase its probability at all. More formally, the problem is just that if P(d_k ) = 0 then P(d_k / s) = 0. Therefore, if Bayesian induction is possible at all, the hypothesis must have a prior probability greater than zero, i.e. P(d_k ) > 0. It follows logically that some constraint on the range of possible hypotheses is required for, according to the Principle of Indifference, prior to any empirical evidence, every hypothesis must be awarded equi-probability. If the range of hypotheses were infinite, then, every hypothesis across the infinite range must be awarded equi-probability, which cannot in sum exceed 1. But in any such case most hypotheses in the range must possess a zero value and, therefore, Bayesian reasoning could never get off the ground.

This particular objection can easily be met. Certainly, in order to exploit Bayes's Theorem as I have suggested, the clinician must be able to determine prior probabilities for hypotheses but, as I have shown, the clinician could generate initial sets of diagnostic hypotheses on the basis of crude frequencies in defined populations of patients and subsequently consider those hypotheses as a basis for subjective appraisal.

Further, the number of hypotheses considered at any one time by the clinician will be strictly limited if only for purely practical reasons. ³⁰ In actual medical practice, therefore, the range of hypotheses will always be constrained to some finite number. Moreover, the point here is not merely a pragmatic one. Rather, it is methodological, i.e. application of the principles of prudence and parsimony outlined in Section IV ensures that, in any given case, Bayesian induction will get off the ground.

The second objection may initially seem more worrying. It is as follows: The proper application of Bayes's Theorem presupposes the independence of pieces of evidence. In the present context, this implies that symptoms should be independent one from another. But that is not always the case. As Knill Jones (1988) notes, for example, in the diagnosis of jaundice, symptoms such as passing dark urine and passing pale stools are highly correlated, i.e. these symptoms are certainly not independent. The worry is, then, that the completely uncritical use of Bayes's Theorem can, in fact, be highly misleading. As a result, the naive and uncritical application of the theorem in the process of diagnosis has come to be known in the literature (almost affectionately) as 'Idiot's Bayes'.

There are a number of points which need to be made here, however. As Macartney (1995) notes, the uncritical assumption of independence of symptoms:"..has not prevented outperformance of skilled clinicians. It has recently been demonstrated by computer simulation that near optimal diagnostic accuracy can be obtained with a training set of 10⁵ cases simply by applying Bayes's Theorem with the usual assumption of conditional independence." ³¹

Hence, the extent to which the clinician will be misled by the uncritical application of Bayes's Theorem may well have been significantly exaggerated. Further, this objection is not so much an objection to Bayesianism per se as a complaint about certain Bayesians. As noted, in many cases clinicians are certainly aware of interdependent symptoms and can restrict their applications of Bayes's Theorem accordingly. Indeed, a variety of mathematical techniques are available to the clinician if the need to adjust the weighting of certain symptoms against others arises in a given context. Admittedly, some of the available techniques are complex, e.g. Multivariate Analysis (as illustrated, for example, in Macartney 1995). However, others such as Logistic Regression are relatively simple to apply (as illustrated in Knill Jones 1988).

In essence I have argued that the logic of diagnosis can only be an inductive logic, i.e. a logic which is not confined to 0 and 1 but extends to the interval between those limits. In the present Section however I consider a final attempt to close down the space in which that logic has its being. This attempt arises from a discussion of the nature of the disease taxonomy given in Wulff et al. (1986), Chapter 6. There Wulff laments the lack of precise definitions of the names of diseases and argues that a number of diagnostic problems: "could be solved by establishing clinical working definitions, which would ensure that at least clinical research workers base their diagnoses on similar criteria". ³²

It is tempting to see in this plea a future programme for a tidying up or tightening up of the definitions of the names of diseases in the disease taxonomy which could eliminate the need for inductive reasoning altogether, i.e. by redefining the nomenclature of disease such that observation-statements describing the presence of specific symptoms thereby describe necessary and sufficient conditions for specific diagnostic hypotheses. In fact, we find precisely this possibility discussed in a number of passages in the work of the later Wittgenstein. In The Blue Book, for example, Wittgenstein (1972) explicitly introduces a distinction between symptoms as purely empirical evidence for a disease and criteria which contribute to the definition of the name of that disease and so to the sense or meaning of that name. Having drawn the distinction, Wittgenstein considers two examples, namely, those of toothache and angina. The toothache case is misleading, toothache being a symptom rather than a cause but the example is instructive as regards the nature of criteria:

The terms criterion/criteria are introduced in The Blue Book as ways of getting to know that such and such is the case. Further, these terms are explicitly contrasted with symptoms although both are described as possible warrants for claims to knowledge. However, the question that must be asked here is just whether or not descriptions of the satisfaction of criteria for a given diagnostic hypothesis, d, actually entail that d? In other words, we must clearly distinguish between descriptions of the satisfaction of criteria which warrant a defeasible assertion that d and descriptions of defining characteristics of d which entail that d. If descriptions of the satisfaction of criteria for d do entail that d then, of course, the criterial assertion cannot be a defeasible one, i.e. if the assertion is defeasible it follows that it is possible for the criteria to be satisfied without that for which they are criterial being in fact the case. If the description of the satisfaction of criteria for d does logically entail that d, of course, that is just what is not possible.

However, it is not immediately obvious that Wittgenstein is drawing this distinction in his discussion of angina in The Blue Book. Certainly, it is possible that he intends that satisfaction of the bacillus-criterion should be considered to entail that the patient has angina. But the matter is not quite as simple as this. It is not immediately obvious that the angina case is one of entailment.

Suppose it is discovered that some people who have the bacillus do not have angina, yet, in the vast majority of cases of angina, the bacillus is present. Further suppose that the presence of the bacillus continues to constitute a working defining criterion for angina and forms the basis of continuing diagnostic practices; though it is noted that there are a small number of exceptions. Given that defeating conditions have been specified, how can a description of the presence of the bacillus possibly be understood as entailing that the patient has angina? Alternately, suppose a small number of cases of angina are discovered in which the bacillus is not found. The presence of the bacillus remains the primary diagnostic indicator, the defining criterion, though exceptions are noted. In short, it is unclear whether or not the angina example is intended to be an example of entailment, i.e. one which is meant to preclude defeasibility. Is the term 'defining criterion' to be understood in the technical sense of strictly definitional characteristics? It is by no means clear that Wittgenstein's point is the technical one. Defeasible and non-defeasible grounds are both grounds nonetheless and both are ways of getting to know.

Moreover, there is a clear analogy here with the type of case discussed in Section V, i.e. the diagnosis of hepatocellular carcinoma. There, we supposed that the clinician performed a relevant diagnostic test, namely, determination of alpha-fetoprotein in the serum. Suppose we follow Wulff's suggestion and specify that a positive test is not merely symptomatic but criterial for a diagnosis of hepatocellular carcinoma. As a result we will be forced to recognise both kinds of defeating-conditions outlined above, i.e. it is both the case that 2% of patients who do not have a hepatocellular carcinoma show a positive test and that 30% of patients with hepatocellular carcinoma show a negative result. But this kind of criterial warrant cannot possibly be identical with classical entailment. Classical entailment is monotonic, i.e. it obeys the following metalogical principle (often described as thinning):